Introduction
Did Interstellar present a scientifically accurate depiction of black holes, time dilation, and wormholes, or was it primarily a work of fiction? In this post, I examine the extent to which the film adheres to established physical principles and where it deviates from known scientific models. The work of Christopher Nolan and physicist Kip Thorne resulted in a science fiction film that integrates real physics to an unprecedented degree. Unlike many cinematic portrayals of astrophysical phenomena, Interstellar is grounded in general relativity, gravitational lensing, and black hole physics.
Kip Thorne, a Nobel Prize-winning physicist, played a key role in shaping the film’s scientific foundation. His expertise in relativistic physics guided the depiction of black holes, gravitational time dilation, and wormholes, concepts that are central to both the narrative and the real-world physics of space and time. His collaboration with the visual effects team led to the development of Double Negative Gravitational Renderer (DNGR), a simulation tool that produced the most realistic black hole ever depicted in film all the visual work was produced in IMAX quality, as Christopher Nolan intended from the beginning of the scene production. , as seen in Figure 1.1 that showcases gravitational lensing effects.

Figure 1.1: A scientifically accurate depiction of a black hole's accretion disk
The results were so precise that they contributed to new scientific research, including publications on gravitational lensing effects in Classical and Quantum Gravity Classical and Quantum Gravity is a peer-reviewed scientific journal covering research on general relativity, quantum gravity, black holes, cosmology, and gravitational waves. It publishes theoretical and experimental studies related to spacetime and gravity. See more on the reference [2]. .
The physics of Interstellar
General relativity and the Einstein field equations
The physics behind Interstellar is primarily based on Einstein’s general theory of relativity look at these if you’re curious. , which describes how mass and energy warp spacetime. At the heart of this theory are the Einstein field equations:
$$ R_{\mu\nu} - \frac{1}{2} R g_{\mu\nu} + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4} T_{\mu\nu} $$
where \( R_{\mu\nu} \) is the Ricci curvature tensor, \( R \) is the Ricci scalar, \( g_{\mu\nu} \) is the metric tensor that defines spacetime geometry, \( T_{\mu\nu} \) is the stress-energy tensor representing matter and energy, \( G \) is Newton’s gravitational constant, \( c \) is the speed of light, and \( \Lambda \) is the cosmological constant.

Figure 2.1: An artistic visualization of the star S0-2 as it passes by the supermassive black hole at the galactic center, which has warped the geometry of space and time
The Schwarzschild metric and its limitations
One of the most significant solutions to these equations describes black holes, which are modeled mathematically by the Schwarzschild metric for non-rotating black holes:
$$ ds^2 = -\left( 1 - \frac{2GM}{c^2 r} \right)c^2 dt^2 + \left( 1 - \frac{2GM}{c^2 r} \right)^{-1} dr^2 + r^2 d\Omega^2 $$
where \( M \) is the mass of the black hole, \( r \) is the radial coordinate, and \( d\Omega^2 \) represents the angular components of the metric. However, the black hole in Interstellar, Gargantua, is rotating, requiring the more complex Kerr metric, which accounts for angular momentum.

Figure 2.2: Karl Schwarzschild
The Kerr metric: rotating black holes
So, while the Schwarzschild metric provides a solution for non-rotating black holes, it does not describe black holes that possess angular momentum. Most astrophysical black holes, formed from the collapse of massive stars, are expected to rotate due to the conservation of angular momentum. For such cases, the Kerr metric, derived by Roy Kerr in 1963, is the correct solution to Einstein’s field equations.
The Kerr metric describes the spacetime around a rotating, uncharged black hole and is given by:
$$ds^2 = - \left( 1 - \frac{2GMr}{\Sigma c^2} \right)c^2 dt^2 - \frac{4GMar \sin^2 \theta}{\Sigma c^2} dt d\phi + \frac{\Sigma}{\Delta} dr^2 + \Sigma d\theta^2 + \left( r^2 + a^2 + \frac{2GM a^2 r \sin^2 \theta}{\Sigma c^2} \right) \sin^2 \theta d\phi^2$$
where:
- \( M \) is the mass of the black hole.
- \( a = \frac{J}{Mc} \) is the spin parameter, where \( J \) is the angular momentum.
- \( \Sigma = r^2 + a^2 \cos^2 \theta \) defines the spatial structure.
- \( \Delta = r^2 - \frac{2GMr}{c^2} + a^2 \) determines the event horizon structure.
Event horizons in the Kerr metric
Unlike a Schwarzschild black hole, which has a single event horizon, a Kerr black hole has two, the outer event horizon (\( r_+ \)) and the inner event horizon (\( r_- \)).
These horizons are given by:
$$ r_{\pm} = \frac{GM}{c^2} \pm \sqrt{\frac{G^2 M^2}{c^4} - a^2} $$
where:
- \( r_+ \), the outer event horizon, is the point beyond which no information escapes.
- \( r_- \), the inner horizon, is where spacetime properties become highly unstable.
If \( a = 0 \), meaning the black hole is non-rotating, the equation reduces to the Schwarzschild radius \( r_s = \frac{2GM}{c^2} \). However, when \( a \) increases, the event horizons shrink, and at maximum spin \( a = GM/c^2 \), the two horizons merge into one if the spin parameter aa exceeds the maximum limit, a naked singularity may form instead of a black hole. This would create a region where the gravitational field becomes infinitely strong, and spacetime curvature would be infinite. A naked singularity would violate the cosmological censorship conjecture, which asserts that singularities should not be visible to observers. .
Frame-dragging and the ergosphere
One of the most dramatic effects introduced by rotation is frame-dragging, where spacetime itself is pulled along by the rotation of the black hole. This phenomenon creates an ergosphere, a region outside the event horizon where objects can no longer remain stationary relative to distant observers.
The outer boundary of the ergosphere, known as the static limit, is given by:
$$ r_e = \frac{GM}{c^2} + \sqrt{\frac{G^2 M^2}{c^4} - a^2 \cos^2 \theta} $$
Within this region:
- Any object must co-rotate with the black hole due to frame-dragging.
- The normal rules of stationary motion break down.
- Energy extraction from the black hole becomes theoretically possible.
The Penrose Process, proposed by Roger Penrose in 1969, suggests that particles entering the ergosphere can gain energy from the black hole’s rotation, effectively allowing for energy extraction from black holes. This process has been proposed as a possible mechanism for extracting rotational energy from astrophysical black holes.
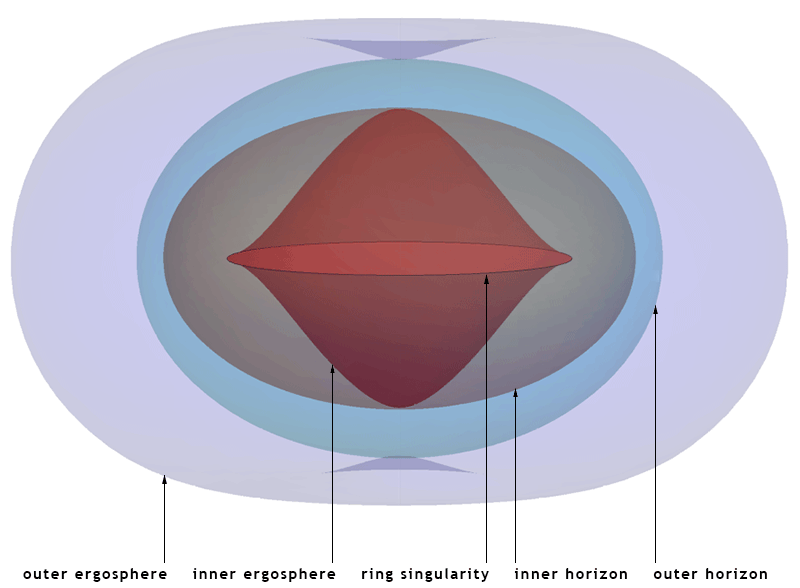
Figure 2.3: Location of the horizons, ergospheres and the ring singularity of the Kerr spacetime in Cartesian Kerr-Schild coordinates
Light and geodesics near a Kerr black hole
In a Schwarzschild black hole, light follows geodesic paths that bend due to gravity. In a Kerr black hole, these paths are even more complex due to the effects of frame-dragging.
Light that orbits a Kerr black hole can exist in two separate photon spheres:
- Prograde orbit: light moving in the same direction as the black hole’s spin can orbit closer due to frame-dragging.
- Retrograde orbit: light moving against the black hole’s spin orbits at a larger distance.
The innermost stable circular orbit (ISCO), the closest orbit that matter can take before falling into the black hole, depends on spin. For a maximally spinning black hole, the ISCO can shrink to just 1 gravitational radius (\( r = GM/c^2 \)), compared to 6 gravitational radii for a Schwarzschild black hole. In Figure 2.4 the spin parameter \( a = 0.999M \).

Figure 2.4: A trapped, unstable, prograde photon orbit just outside the horizon of a spinning black hole
Geodesic equations and motion in curved spacetime
In General relativity, the motion of free-falling objects, including light, follows geodesics, the shortest paths in curved spacetime. The equation governing these trajectories is:
$$ \frac{d^2 x^\mu}{d\tau^2} + \Gamma^\mu_{\alpha\beta} \frac{dx^\alpha}{d\tau} \frac{dx^\beta}{d\tau} = 0 $$
where:
- \( x^\mu \) represents spacetime coordinates (time, space).
- \( \tau \) is the proper time for massive particles (or an affine parameter for light).
- \( \Gamma^\mu_{\alpha\beta} \) are the Christoffel symbols, which encode the effects of curved spacetime on the motion of objects.
For light traveling near a black hole, we set the proper time \( d\tau \) to zero (since photons move along null geodesics), simplifying the equation to describe the path of light around the black hole.
Gravitational lensing and photon orbits
The extreme curvature of spacetime around Gargantua bends the trajectory of light, creating gravitational lensing, where light from background stars (or the black hole’s own accretion disk) is warped and distorted. The amount of bending depends on the impact parameter \( b \), which represents the closest approach distance of a light ray to the black hole.
The deflection angle for a Schwarzschild black hole can be approximated for large impact parameters as:
$$ \theta \approx \frac{4GM}{c^2 b} $$
For a Kerr black hole, the bending is much more complex due to frame-dragging. , which causes light paths to differ depending on whether they move in the direction of the black hole’s spin or against it.
The effective potential for photon motion around a Kerr black hole is given by:
$$ V_{\text{eff}} = \frac{1}{2} \left( 1 - \frac{2GMr}{\Sigma c^2} - \frac{a^2 E^2}{\Sigma c^2} \right) $$
where \( E \) is the energy of the photon, and \( \Sigma \) is the usual Kerr metric term:
$$ \Sigma = r^2 + a^2 \cos^2 \theta $$
This equation determines whether light can escape, orbit, or fall into the black hole.
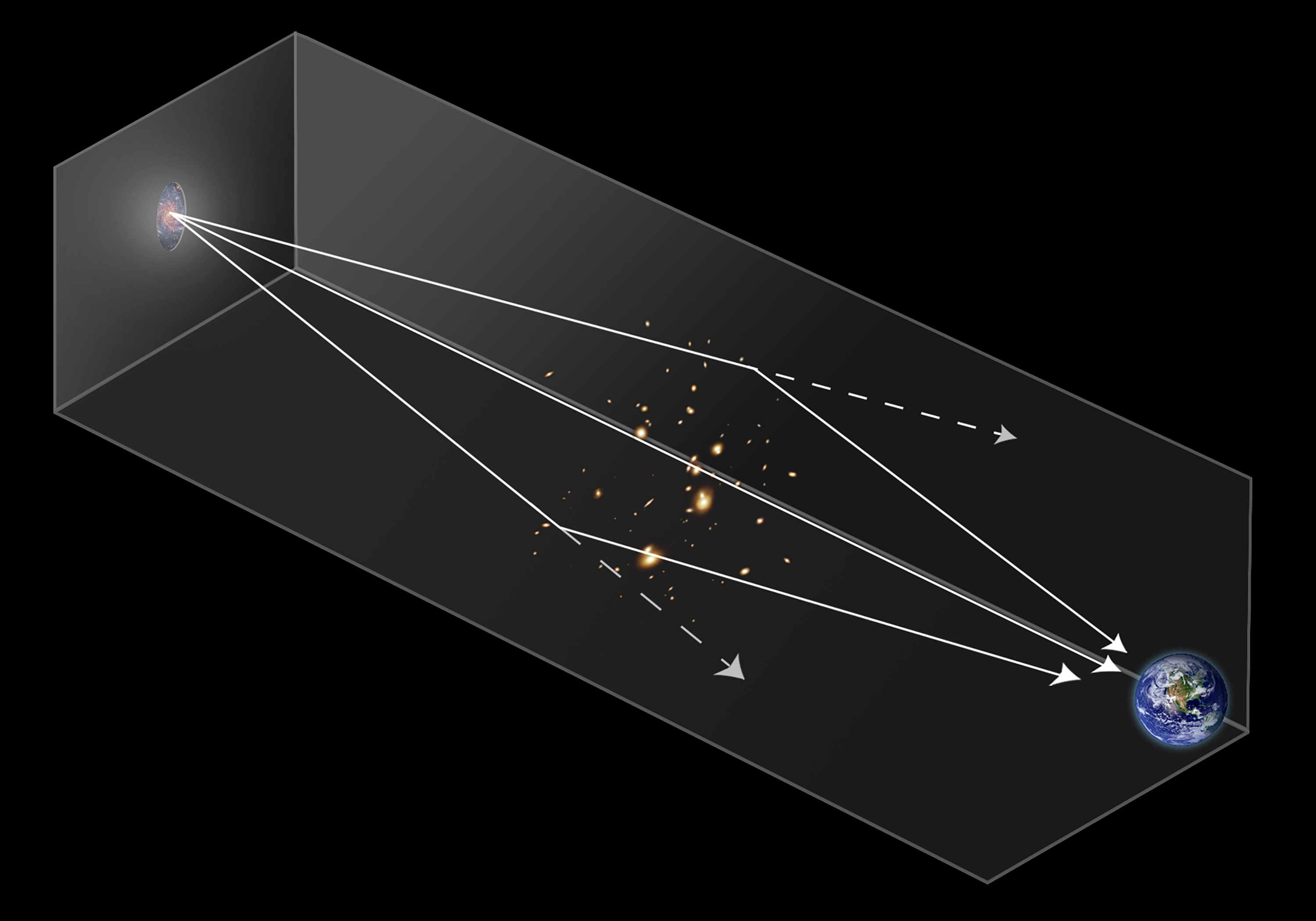
Figure 2.5: Gravitational lensing diagram illustrating how rays of light from a distant galaxy or star can be bent by the gravity of an intervening galaxy cluster
Time dilation and gravitational effects in Interstellar
One of the most fascinating and extreme predictions of general relativity is gravitational time dilation I also discussed gravity time dilation here and here. , the slowing of time in strong gravitational fields. This effect is not merely a theoretical curiosity, it has been confirmed through numerous experiments, including observations of GPS satellite clocks running slightly faster than those on Earth’s surface due to weaker gravity at higher altitudes.
In Interstellar, time dilation is crucial to the plot, especially when the crew visits Miller’s planet, a world orbiting dangerously close to the massive black hole Gargantua. Here, time is stretched to an extreme: one hour on the planet is equivalent to seven years on Earth. This raises several important questions:
- Can such extreme time dilation really occur?
- What equations govern gravitational time dilation?
- How does a rotating black hole like Gargantua affect time dilation compared to a non-rotating one?
Gravitational time dilation and the Schwarzschild metric
The simplest way to describe time dilation is through the Schwarzschild metric, which I discussed in Chapter 2.2. The proper time experienced by a stationary observer in a gravitational field (relative to a distant observer) is given by:
$$ \Delta t’ = \Delta t \sqrt{1 - \frac{2GM}{c^2 r}} $$
where:
- \( \Delta t' \) is the dilated time experienced by an observer in a strong gravitational field.
- \( \Delta t \) is the proper time experienced by a faraway observer at infinity.
- \( G \) is Newton’s gravitational constant.
- \( M \) is the mass of the gravitating body (e.g., Gargantua).
- \( c \) is the speed of light.
- \( r \) is the radial distance from the center of the mass.
This equation shows that as an observer moves closer to the event horizon, the time dilation factor approaches zero, meaning time slows infinitely compared to a distant observer.
However, Gargantua is a rapidly rotating Kerr black hole, meaning the Schwarzschild metric is insufficient to fully describe the time dilation effects.
The time dilation equation for rotating black holes
For a Kerr black hole, time dilation is influenced not only by gravity but also by frame-dragging, the effect where space itself is dragged along with the rotating mass. The proper time equation is given by:
$$ \Delta t’ = \Delta t \sqrt{ \frac{r^2 - 2GMr/c^2 + a^2}{r^2 + a^2 \cos^2 \theta} } $$
where:
- \( a = J/Mc \) is the spin parameter of the black hole.
- \( \theta \) represents latitude (0° at the equator, 90° at the poles).
- Other variables retain their previous meanings.
Unlike the Schwarzschild case, where time dilation depends only on distance \( r \), the Kerr metric introduces dependence on both latitude and spin. Near the equatorial plane, the effects of frame-dragging become dominant.
A maximally spinning Kerr black hole (\( a = GM/c^2 \)) can significantly reduce the radius at which extreme time dilation occurs. This allows for a scenario like Miller’s planet, where extreme time dilation exists outside the event horizon.

Figure 3.1: A diagrammatic representation of spacetime
The extreme time dilation on Miller’s planet
In Interstellar, the crew visits Miller’s planet, which orbits extremely close to Gargantua. According to the film, time correspondences implies a time dilation factor of approximately:
$$ \frac{\Delta t}{\Delta t’} = 7 \times 365 \times 24 = 61,320 $$
meaning that for every hour on Miller’s planet, 61,320 hours (7 years) pass for an observer far from Gargantua.
To determine whether this is physically plausible, we solve for \( r \) (the planet’s orbital distance) using the Schwarzschild time dilation equation:
$$ \sqrt{1 - \frac{2GM}{c^2 r}} = \frac{1}{61,320} $$
For Gargantua, which is estimated to be 100 million solar masses (\( M = 10^8 M_{\odot} \)), we substitute:
$$ r \approx \frac{2GM}{c^2} \left( 1 + \frac{1}{61,320^2} \right) $$
Solving this numerically gives an orbital radius extremely close to the event horizon. However, a planet this close would be tidally disrupted by the black hole’s gravitational forces, making it unlikely to exist in reality unless Gargantua’s spin allows for a stable orbit outside the ISCO.
Gravitational redshift and frequency shift
Another effect of extreme gravity is gravitational redshift, where light escaping a strong gravitational field loses energy. The equation is:
$$ z = \frac{1}{\sqrt{1 - \frac{2GM}{rc^2}}} - 1 $$
where \( z \) is the redshift factor. A highly redshifted signal means that light leaving Miller’s planet appears much lower in frequency when observed from a distant location.
This means that:
- Communication signals from Miller’s planet would be stretched and distorted.
- If an astronaut on Miller’s planet looked at the stars, they would appear blue-shifted due to extreme gravitational fields.
Such relativistic redshift effects are well-documented in astrophysics and have been observed in white dwarfs and neutron stars.
Wormholes: the Einstein-Rosen bridge and traversability
In Interstellar, one of the central plot devices is a wormhole, a shortcut through spacetime that allows near-instantaneous travel between two distant regions of the universe. While wormholes are a mathematically valid solution to Einstein’s field equations, their physical existence and stability remain an open question in modern theoretical physics.
The film presents a stable, traversable wormhole, an idea that originates from Einstein and Nathan Rosen’s 1935 paper on bridges in spacetime, later expanded by Kip Thorne and Michael Morris in 1988. However, there are several major challenges that any real-world wormhole would have to overcome:
- Can wormholes exist naturally, or must they be artificially created Figure 4.1 is in two-dimensional space. A three-dimensional representation would require a fourth spatial dimension, popularly known as hyperspace. ?
- How can they be stabilized to prevent collapse?
- Do they require exotic matter to remain open?
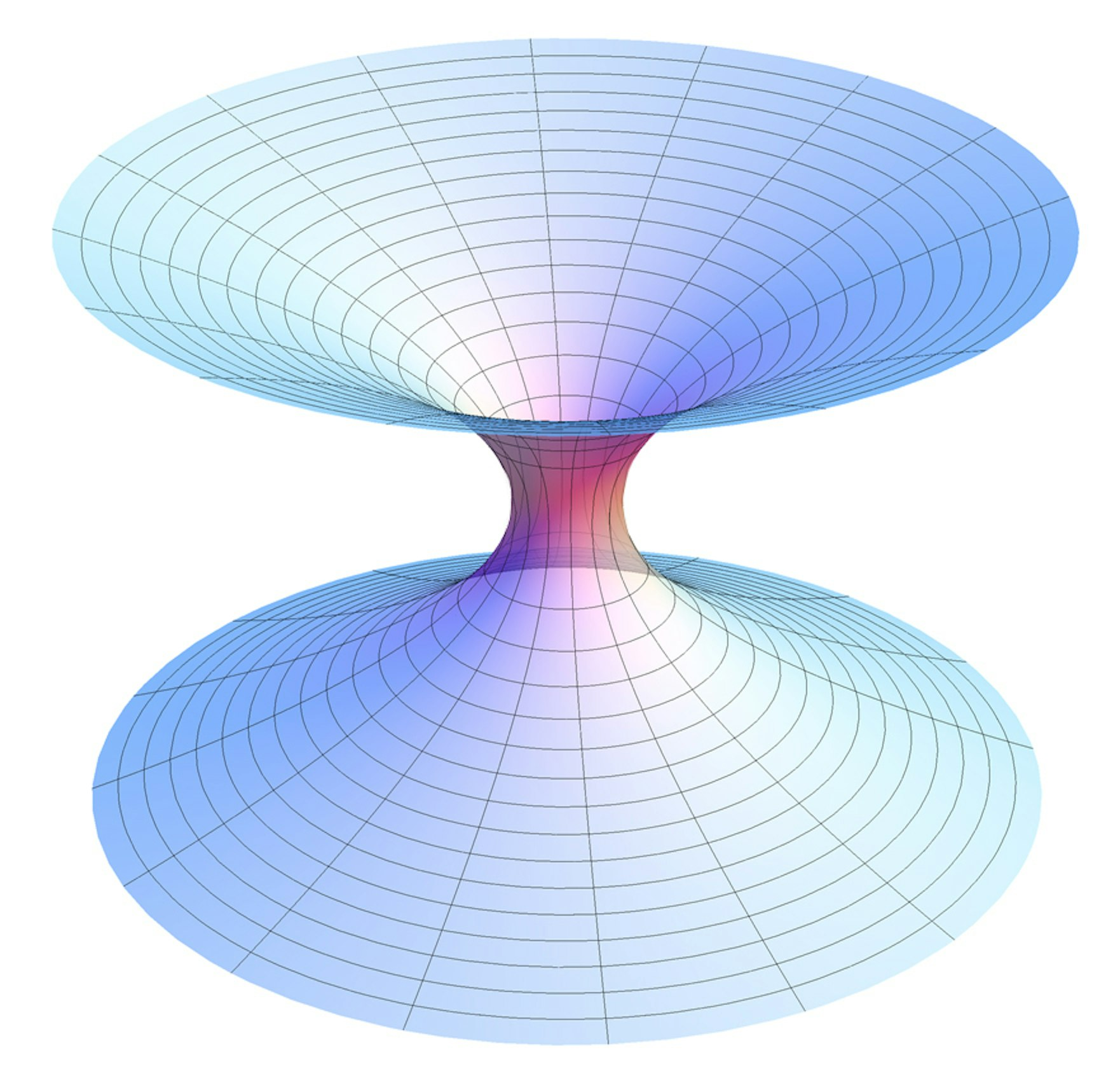
Figure 4.1: A diagram of what a wormhole might look like
Theoretical foundations of wormholes
The Einstein field equations allow for solutions where spacetime forms a tunnel-like structure connecting two distant points. This idea, first proposed by Einstein and Rosen (1935), describes what is now called the Einstein-Rosen bridge, mathematically represented as a Schwarzschild wormhole while the Einstein-Rosen bridge is often associated with wormholes, its original formulation describes a connection between two black holes rather than a traversable shortcut. In fact, the Einstein-Rosen bridge is just a mathematical extension of the maximally extended Schwarzschild solution, see more on the reference [8]. . However, it is not traversable because:
- It collapses too quickly for anything to cross.
- It requires exotic matter to remain open.
To create a traversable wormhole, a more advanced model is needed, specifically the Morris-Thorne metric.

Figure 4.2: Albert Einstein and Nathan Rosen
The energy conditions for traversable wormholes
In 1988, Michael Morris and Kip Thorne introduced a traversable wormhole metric, designed to allow passage without violating known physics. The Morris-Thorne metric is:
$$ ds^2 = -c^2 dt^2 + dl^2 + (b^2 + l^2)(d\theta^2 + \sin^2\theta d\phi^2) $$
where:
- \( b \) is the wormhole throat radius.
- \( l \) is the proper radial distance along the wormhole.
Unlike the Einstein-Rosen bridge, this wormhole is designed to remain open. However, its stability requires violating the null energy condition (NEC).
The null energy condition and exotic matter
The null energy condition (NEC) states that for any light-like observer with four-velocity \( k^\mu \), the energy-momentum tensor must satisfy:
$$ T_{\mu\nu} k^\mu k^\nu \geq 0 $$
However, for a wormhole to stay open, the metric requires negative energy density, meaning:
$$ T_{\mu\nu} k^\mu k^\nu < 0 $$
This implies the need for exotic matter, a form of energy with negative mass-energy density.
Does exotic matter exist?
- Casimir Effect: In quantum field theory, the Casimir effect demonstrates that vacuum fluctuations can produce negative energy densities when two uncharged, parallel metal plates are placed very close together, they alter the quantum vacuum fluctuations between them, creating a region of lower energy density, effectively producing negative energy relative to the surrounding space. , but at very small scales.
- Quantum Gravity Hypotheses: Some theories the so-called “quantum inequalities” suggest that negative energy exists, but only in small, temporary amounts. suggest that quantum effects near Planck-scale physics could generate violations of the NEC, potentially allowing stable wormholes.
- Dark Energy Connection?: Some researchers speculate that the same unknown force responsible for the universe’s accelerated expansion (dark energy) might contribute to negative energy conditions.
While exotic matter is theoretically allowed by quantum field effects, it has never been observed in macroscopic quantities, making wormhole stability a major unresolved issue.
Can wormholes be created and stabilized?
Even if wormholes could exist, the question remains:
- Can we artificially create them?
- Can they remain open long enough for practical travel?
Theoretical construction of a wormhole
To construct a traversable wormhole, one would need to:
- Generate a metric satisfying the Morris-Thorne conditions.
- Introduce enough exotic matter to hold the throat open.
- Control instability caused by small perturbations.
Several speculative proposals exist in modern physics:
- Quantum Gravity Effects: Some models suggest that at the Planck scale (\(10^{-35}\) meters), space itself might fluctuate in a way that allows small wormholes to exist naturally.
- Artificial Wormhole Creation: Theoretically, if we could engineer strong enough gravitational fields, it might be possible to distort spacetime into a wormhole-like configuration.
- Brane World Models: In string theory and higher-dimensional physics (such as Randall-Sundrum models), extra dimensions could naturally allow for wormhole formation.
Higher dimensions and the tesseract Scene
One of the most visually and conceptually abstract sequences in Interstellar occurs when Cooper enters the tesseract, a higher-dimensional construct that allows him to interact with past events in a nonlinear manner. While this may appear to be pure science fiction, it is inspired by real theoretical physics, particularly ideas from string theory, brane-world models, and extra-dimensional gravity.

Figure 5.1: The tesseract scene
Extra dimensions in theoretical physics
Why consider extra dimensions?
In our everyday experience, we perceive three spatial dimensions and one time dimension As illustrated in Flatland, a classic novella by Edwin A. Abbott, beings in a two-dimensional world would struggle to comprehend a third dimension, just as we might struggle to visualize additional spatial dimensions beyond our own. . However, many advanced physical theories propose the existence of additional spatial dimensions, primarily for two reasons:
- Unifying Fundamental Forces: Theories such as Kaluza-Klein theory and string theory suggest that adding extra dimensions can naturally unify gravity with the other fundamental forces (electromagnetism, strong nuclear, and weak nuclear).
- Solving the Hierarchy Problem: The weakness of gravity compared to the other fundamental forces could be explained if gravity leaks into extra dimensions, as proposed by brane-world models (Randall-Sundrum models).
Kaluza-Klein theory: the first step toward extra dimensions
The first significant proposal for extra dimensions was Kaluza-Klein theory (1921-1926), which attempted to unify gravity and electromagnetism by introducing a fifth spatial dimension. The idea was that Maxwell’s equations (describing electromagnetism) and Einstein’s equations (describing gravity) could emerge from a five-dimensional Einstein field equation:
$$ R_{AB} - \frac{1}{2} R g_{AB} = \frac{8\pi G}{c^4} T_{AB} $$
where:
- \( A, B \) index five-dimensional spacetime (four spatial dimensions + one time dimension).
- When compactifying the extra dimension, electromagnetism emerges naturally.
This was an elegant approach but lacked experimental verification. However, it laid the groundwork for modern string theory and brane-world models.
Brane-world models and gravity leakage
More recently, Randall-Sundrum (RS) models propose that our four-dimensional universe is embedded in a higher-dimensional spacetime. In these models:
- Gravity is stronger in the higher-dimensional bulk but appears weak in our four-dimensional universe because it is “diluted” across extra dimensions.
- This can explain why gravity is so much weaker than electromagnetism without requiring drastic modifications to known physics.
The extra-dimensional bulk proposed in RS models is similar to the fifth-dimensional bulk referenced in Interstellar, where gravity is manipulated across different regions of spacetime.
The mathematics of five-dimensional spacetime
The tesseract scene in Interstellar represents a five-dimensional construct, allowing Cooper to perceive time as a spatial dimension. This concept aligns with some higher-dimensional gravity theories, where:
- Time is not fixed but becomes an additional “direction” in spacetime.
- Movement in this extra-dimensional bulk allows interactions with different points in time.
The 5D metric and extra-dimensional gravity
A five-dimensional extension of General Relativity uses a metric tensor with an extra dimension:
$$ ds^2 = g_{\mu\nu}dx^\mu dx^\nu + g_{44}dx^4 dx^4 $$
where:
- \( g_{\mu\nu} \) describes the familiar four-dimensional metric (our usual spacetime).
- \( g_{44} \) represents the extra-dimensional component.
How does this relate to the tesseract?
In Interstellar:
- The bulk beings (interpreted as future humans or higher-dimensional entities) allow Cooper to experience all moments in time as spatially connected locations.
- The tesseract is a higher-dimensional structure that represents time as a navigable dimension, allowing Cooper to interact with past events via gravity.
Is this physically possible?
While there is no experimental evidence that we can interact with time in this way, similar ideas exist in:
String theory, which requires 10 or 11 dimensions. Figure 5.2 depicts a cross-section of a quintic Calabi–Yau manifold, a special type of geometric space important in string theory. These manifolds provide the extra spatial dimensions required in certain versions of superstring theory, helping to unify gravity with quantum mechanics.
Brane-world models, where higher-dimensional beings could theoretically manipulate spacetime curvature.
The AdS/CFT correspondence, which suggests that physics in a lower-dimensional space may be governed by higher-dimensional physics.

Figure 5.2: A cross section of a quintic Calabi–Yau manifold
The feasibility of interstellar travel
One of the most ambitious ideas explored in Interstellar is the possibility of humanity traveling beyond our solar system to find a new home Professor Brand tells Cooper, in their first meeting, that the Lazarus missions have been sent out to search for new homes for humanity. Cooper responds, “There’s no planet in our solar system that can support life, and it’d take a thousand years to reach the nearest star. That doesn’t even qualify as futile. Where did you send them, Professor?” The worse-than-futile challenge, if you don’t have a wormhole, is obvious when you realize just how far it is to the nearest stars. . While interplanetary travel within our own solar system is an active area of research, interstellar travel remains a much greater challenge due to the vast distances involved.
The energy requirements for interstellar travel
The problem of distance and speed
The nearest known exoplanet, Proxima Centauri b, is 4.24 light-years away. This means that even at the speed of light, a journey would take 4.24 years:
However, current space technology operates at a tiny fraction of light speed. For example:
| Spacecraft | Speed (relative to c) | Time to Proxima b |
|---|---|---|
| Voyager 1 | 0.00006c | 73,000 years |
| New Horizons | 0.0001c | 42,000 years |
| Breakthrough Starshot (planned) | 0.2c | 20 years |
To make interstellar travel feasible, we need speeds much closer to c, requiring enormous amounts of energy.
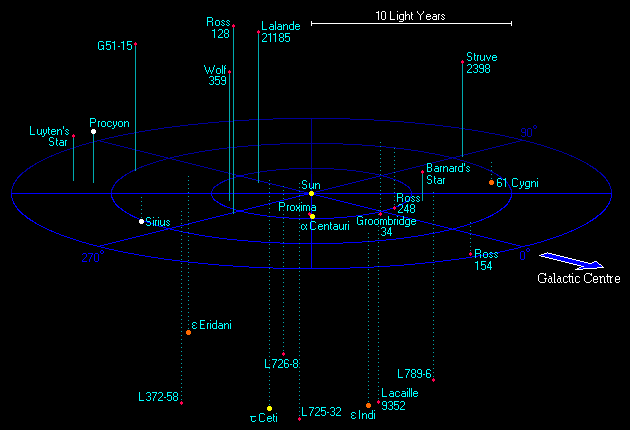
Figure 6.1: All the stars within 12 light-years of Earth
The Tsiolkovsky rocket equation
A conventional rocket must carry both fuel and oxidizer, meaning that for every unit of fuel burned, only a fraction contributes to acceleration. The Tsiolkovsky rocket equation governs this limitation:
$$ \Delta v = v_e \ln{\frac{m_0}{m_f}} $$
where:
- \( \Delta v \) is the change in velocity.
- \( v_e \) is the exhaust velocity of the propellant.
- \( m_0 \) is the initial mass of the spacecraft (including fuel).
- \( m_f \) is the final mass (after burning fuel).
To reach relativistic speeds (e.g., 0.2c), a spacecraft using chemical propulsion would require an absurd fuel mass ratio, far beyond anything practical. Alternative propulsion methods must be explored.

Figure 6.2: Konstantin Eduardovich Tsiolkovsky
Alternative propulsion technologies
Several advanced propulsion concepts have been proposed for interstellar travel:
- Nuclear Fusion Rockets: fusion reactions could provide higher exhaust velocity, making them far more efficient than chemical rockets.
- Antimatter Propulsion: annihilating matter with antimatter releases enormous energy, but antimatter is extremely difficult to produce and store.
- Light Sail Propulsion: the Breakthrough Starshot Initiative proposes using laser-driven light sails to push small spacecraft to ~0.2c.
While these methods show promise, none currently offer a realistic pathway to human interstellar travel. Faster-than-light (FTL) travel would be required, which leads us to warp drives.
The Alcubierre warp drive: a realistic alternative?
Faster-than-light travel and relativity
According to Einstein’s special relativity, the speed of light (\( c \)) is the ultimate speed limit for any object with mass:
$$ E = \gamma mc^2, \quad \gamma = \frac{1}{\sqrt{1 - v^2/c^2}} $$
where \( \gamma \) is the Lorentz factor, which increases toward infinity as velocity approaches c, making it impossible to reach or exceed light speed with conventional means.
However, general relativity does not forbid spacetime itself from moving faster than light. This is the idea behind the Alcubierre warp drive, first proposed in 1994.

Figure 6.3: Two-dimensional visualization of an Alcubierre drive, showing the opposing regions of expanding and contracting spacetime that displace the central region
The Alcubierre metric
The Alcubierre metric describes a spacetime configuration that allows a “warp bubble” to move faster than light:
$$ ds^2 = -c^2 dt^2 + (dx - v_s f(r_s) dt)^2 + dy^2 + dz^2 $$
where:
- \( v_s \) is the velocity of the warp bubble.
- \( f(r_s) \) is a smooth function that defines the bubble’s shape.
This solution contracts space in front of the bubble and expands space behind it, allowing the ship inside to travel faster than light relative to an external observer, without violating Special Relativity.
Problems with the warp drive
Despite being mathematically valid, the Alcubierre drive faces major challenges:
- Exotic Matter Requirement: The warp drive needs negative energy density (violating the NEC), similar to a traversable wormhole.
- Energy Costs: Early estimates suggested that creating a warp bubble would require the total energy of an entire star, though newer models suggest reducing this.
- Quantum Instabilities: The interaction of a warp bubble with surrounding spacetime could cause destructive radiation effects.
Currently, the Alcubierre drive remains purely theoretical, but it is one of the most serious FTL concepts explored in modern physics.
Habitability and exoplanets: could we find another Earth?
Even if interstellar travel becomes feasible, the next challenge is finding a habitable planet.
Exoplanet detection and the habitable zone
A habitable exoplanet must meet several criteria:
- Located in the habitable zone (where liquid water can exist).
- Similar size and atmosphere to Earth.
- Magnetic field to protect from cosmic radiation.
- Stable orbit and climate conditions.
The most promising exoplanets discovered so far include:
| Exoplanet | Distance (light-years) | Habitability Potential |
|---|---|---|
| Proxima Centauri b | 4.24 | High (but exposed to radiation) |
| Kepler-442b | 1,120 | High (Earth-like, in habitable zone) |
| TOI-700d | 101 | Moderate (potentially rocky) |
Could planets like Cooper station exist?
In Interstellar, humanity eventually colonizes Cooper station, a massive space station orbiting Saturn. While space habitats are a more immediate solution than interstellar travel, sustaining human life on an exoplanet would require:
- Terraforming technology to modify atmospheric conditions.
- Self-sustaining biospheres for food and oxygen.
- Long-term radiation protection from stellar activity.
Currently, no exoplanets are confirmed to be fully Earth-like, but new discoveries (such as TRAPPIST-1 planets) continue to offer hope.
Conclusion: scientific accuracy vs. cinematic liberties
What Interstellar got right
Interstellar is one of the most scientifically ambitious science fiction films ever made. Its depiction of the black hole Gargantua is one of the most scientifically accurate visualizations of a black hole ever created for film. The simulation was based on general relativity equations, solved numerically using the Double Negative Gravitational Renderer (DNGR). The film correctly portrays gravitational lensing, where light bends around the black hole due to spacetime curvature. It also incorporates the Kerr metric, which describes a rotating black hole, and accurately simulates the appearance of an accretion disk, where relativistic Doppler boosting and gravitational redshift influence the brightness and color of the disk.
Time dilation on Miller’s planet is another example of real physics being applied in the film. The Kerr metric allows for extreme time dilation near a spinning black hole, and gravitational redshift effects were correctly included in the film’s depiction. While the exact seven-year-per-hour ratio may be exaggerated, the concept is grounded in relativity.
The wormhole in the film follows the Morris-Thorne model, a valid solution to Einstein’s equations. The film correctly acknowledges that negative energy density is required to keep a wormhole open, and the gravitational lensing effects around the wormhole entrance are consistent with how light would behave in such a scenario.
The concept of higher dimensions, as presented in the tesseract scene, is inspired by brane-world models and string theory. The idea that gravity could interact across extra dimensions is a real topic of research in theoretical physics, and some models suggest that higher-dimensional beings or future humans could manipulate gravity in ways that affect time and space.
Where Interstellar took creative liberties
Despite its strong scientific foundation, the film exaggerates certain effects for dramatic purposes.
The extreme time dilation on Miller’s planet would require the planet to orbit extremely close to the event horizon while remaining stable and habitable. In reality, such a planet would likely experience extreme tidal forces that could tear it apart unless it was in a finely tuned orbit around a rapidly spinning black hole.
The wormhole’s stability and placement near Saturn is another major artistic liberty. In theoretical physics, wormholes require exotic matter to remain open, and even then, they might be unstable and short-lived. The idea that an advanced civilization could create and stabilize a wormhole in a fixed location for decades is highly speculative.
The most scientifically questionable moment in the film is Cooper’s survival inside the black hole. The film presents the idea that he enters a higher-dimensional space where he can perceive time as a navigable dimension. In reality, any object crossing the event horizon of a black hole would likely experience spaghettification due to extreme tidal forces. Some theoretical models suggest that a Kerr black hole might contain a “gentle singularity” that does not destroy matter instantly, but this remains purely speculative.
Figure 7.1: Astronaut falling into a black hole (spaghettification effect)
The influence of Interstellar on scientific discussions
Since its release, Interstellar has increased public interest in general relativity, black holes, and time dilation. The film’s depiction of Gargantua contributed to a scientific paper on gravitational lensing around Kerr black holes, demonstrating that Hollywood visual effects can have real scientific applications.
The film has also sparked renewed discussions on wormholes and faster-than-light travel. While still speculative, these topics have gained more visibility in scientific literature and public discourse.
Interstellar is not a physics textbook, but it successfully introduces audiences to complex scientific ideas in a compelling way. The film serves as a gateway into the study of general relativity, astrophysics, and cosmology.
Figure credits
Figure 1.1: Double Negative artists/DNGR/TM&© Warner Bros. Entertainment Inc./Creative Commons (CC BY-NC-ND 3.0) license.
Figure 2.1: National Science Foundation graphic by Nicolle R. Fuller.
Figure 2.4: Gravitational Lensing by Spinning Black Holes in Astrophysics, and in the Movie Interstellar, Oliver James, Eugénie von Tunzelmann, Paul Franklin, and Kip S. Thorne.
Figure 2.5: NASA, ESA, Ann Feild (STScI), Frank Summers (STScI)
Figure 5.1: Double Negative artists/DNGR/TM&© Warner Bros. Entertainment Inc./Creative Commons (CC BY-NC-ND 3.0) license.
Figure 6.1: Richard Powell.
Figure 6.3: Wikipedia, CC BY-SA 3.0.
Other Figures: public domain.
References
[1] Kip S. Thorne, The Science of Interstellar, W. W. Norton & Company, New York, 2014.
[2] Oliver James, Eugénie von Tunzelmann, Paul Franklin, and Kip S. Thorne, Gravitational Lensing by Spinning Black Holes in Astrophysics, and in the Movie Interstellar. Classical and Quantum Gravity, vol. 32, no. 6, 2015, 065001.
[3] Oliver James, Eugénie von Tunzelmann, Paul Franklin, and Kip S. Thorne, Visualizing Interstellar’s Wormhole. American Journal of Physics, vol. 83, no. 6, 2015, pp. 486–499.
[4] IMDb, Interstellar, 2014.
[5] Quora, What are some of the most fascinating instances of attention to detail in movies?.
[6] Charles W. Misner, Kip S. Thorne, John A. Wheeler, Gravitation, W. H. Freeman, 1973.
[7] Michael S. Morris, Kip S. Thorne, Wormholes in Spacetime and Their Use for Interstellar Travel, American Journal of Physics, 1988.
[8] Albert Einstein, Nathan Rosen, The Particle Problem in the General Theory of Relativity, Physical Review, vol. 48, 1935, pp. 73-77.
[9] Stephen W. Hawking, Chronology Protection Conjecture, Physical Review D, vol. 46, no. 2, 1992, pp. 603-611.
[10] Lisa Randall, Raman Sundrum, A Large Mass Hierarchy from a Small Extra Dimension, Physical Review Letters, vol. 83, no. 17, 1999, pp. 3370–3373.
[11] Juan M. Maldacena, The Large-N Limit of Superconformal Field Theories and Supergravity, Advances in Theoretical and Mathematical Physics, vol. 2, 1998.
[12] Edwin A. Abbott, Flatland: A Romance of Many Dimensions, 1884.